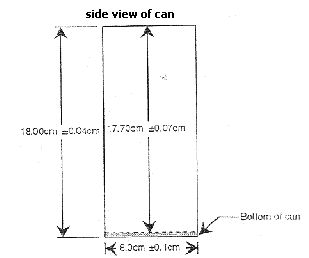
Questions1) Calculate the volume of the bottom of the cylindrical can in
Fig. 0.1. The outside measures
FIGURE 0.1
2) Students in T&AM 203 (Dynamics) can choose between two different procedures when measuring the period of an oscillating weight on a spring. In Procedure A, a timer is started and stopped electronically, as the weight repeatedly passes through a light beam; the error in starting and stopping the timer is negligible. The timer reads in units of 1 millisecond, but is not crystal-controlled, and typically runs 2 percent fast or slow. In Procedure B a regular hand-held digital stopwatch is used, which
reads in units of 0.01 seconds, or 10 ms. Being crystal-controlled,
the stopwatch runs at the correct speed, and is not significantly
fast or slow. However, since it is manually operated, an error of
about Assume that the period of oscillation of the weight is exactly two seconds.
3) A carpenter laying out a 40 foot wall with studs every 16 inches
can't find his long measuring tape, so he carefully cuts a scrap
board to a length of 16 4) Ultrasonic range finders bounce high-frequency pulses of sound
off objects, and time the echoes to determine distance. One popular
model has a range of 0.3 to 10 meters, and (at an air temperature
of 20ºC) gives an echo time of 0.0017 seconds at a distance
of 0.3 meters, and 0.0583 seconds at 10 meters. Based on the way
it works, do you think the device is linear? (Assume uniform air
properties.) If possible, calibrate the range finder by finding
a formula relating echo time to distance. Optional: What else could
you measure with this device?
|
cm,
the inside measures 
cm,
and the diameter measures 
cm.
Assume the errors are independent. Write down your result and its
error, using:
0.1
second is introduced once as the stopwatch is started and again
when it is stopped (assume these errors are independent).|
Main Body
|